Additional details based on what I have found here and there as I was looking for an implication operator : you can use a clever hack to define your own operators. Here is a running example annotated with sources leading me to this result.
#!/usr/bin/python
# From http://code.activestate.com/recipes/384122/ (via http://stackoverflow.com/questions/932328/python-defining-my-own-operators)
class Infix:
def __init__(self, function):
self.function = function
def __ror__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __rlshift__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __or__(self, other):
return self.function(other)
def __rshift__(self, other):
return self.function(other)
def __call__(self, value1, value2):
return self.function(value1, value2)
from itertools import product
booleans = [False,True]
# http://stackoverflow.com/questions/16405892/is-there-an-implication-logical-operator-in-python
# http://jacob.jkrall.net/lost-operator/
operators=[
(Infix(lambda p,q: False), "F"),
(Infix(lambda p,q: True), "T"),
(Infix(lambda p,q: p and q), "&"),
(Infix(lambda p,q: p or q) , "V"),
(Infix(lambda p,q: p != q) , "^"),
(Infix(lambda p,q: ((not p) or not q)), "nad"),
(Infix(lambda p,q: ((not p) and not q)), "nor"),
(Infix(lambda p,q: ((not p) or q)), "=>"),
]
for op,sym in operators:
print "nTruth tables for %s" % sym
print "nptqtp %s qtq %s p" % (sym,sym)
for p,q in product(booleans,repeat=2):
print "%dt%dt%dt%d" % (p,q,p |op| q,q |op| p)
print "nptqtrtp %s qtq %s rt(p %s q) %s rtp %s (q %s r)tp %s q %s r" % (sym,sym,sym,sym,sym,sym,sym,sym)
for p,q,r in product(booleans,repeat=3):
print "%dt%dt%dt%dt%dt%dtt%dtt%d" % (p,q,r,p |op| q,q |op| r, (p |op| q) |op| r, p |op| (q |op| r), p |op| q |op| r)
assert( (p |op| q) |op| r == p |op| q |op| r)
Дополнительные сведения, основанные на том, что я нашел здесь и там, когда я искал оператор импликации: вы можете использовать умный взлом, чтобы определить своих собственных операторов. Ниже приведен пример выполнения, аннотированный источниками, приводящими меня к этому результату.
#!/usr/bin/python
# From http://code.activestate.com/recipes/384122/ (via http://stackoverflow.com/questions/932328/python-defining-my-own-operators)
class Infix:
def __init__(self, function):
self.function = function
def __ror__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __rlshift__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __or__(self, other):
return self.function(other)
def __rshift__(self, other):
return self.function(other)
def __call__(self, value1, value2):
return self.function(value1, value2)
from itertools import product
booleans = [False,True]
# http://stackoverflow.com/questions/16405892/is-there-an-implication-logical-operator-in-python
# http://jacob.jkrall.net/lost-operator/
operators=[
(Infix(lambda p,q: False), "F"),
(Infix(lambda p,q: True), "T"),
(Infix(lambda p,q: p and q), "&"),
(Infix(lambda p,q: p or q) , "V"),
(Infix(lambda p,q: p != q) , "^"),
(Infix(lambda p,q: ((not p) or not q)), "nad"),
(Infix(lambda p,q: ((not p) and not q)), "nor"),
(Infix(lambda p,q: ((not p) or q)), "=>"),
]
for op,sym in operators:
print "nTruth tables for %s" % sym
print "nptqtp %s qtq %s p" % (sym,sym)
for p,q in product(booleans,repeat=2):
print "%dt%dt%dt%d" % (p,q,p |op| q,q |op| p)
print "nptqtrtp %s qtq %s rt(p %s q) %s rtp %s (q %s r)tp %s q %s r" % (sym,sym,sym,sym,sym,sym,sym,sym)
for p,q,r in product(booleans,repeat=3):
print "%dt%dt%dt%dt%dt%dtt%dtt%d" % (p,q,r,p |op| q,q |op| r, (p |op| q) |op| r, p |op| (q |op| r), p |op| q |op| r)
assert( (p |op| q) |op| r == p |op| q |op| r)
На этой странице вы узнаете
- Что не так с импликацией и эквиваленцией?
- Какое применение алгебра логики может найти в программировании?
В статье «Алгебра логики» мы выучили основы этого непростого раздела математики. Разобравшись в той теме, пора пойти дальше и заговорить на понятном компьютеру языке — языке программирования.

Логические уравнения в Python
В Python эта логика сохраняется. В нем есть логический тип данных bool, который может принимать значение True или False — истина и ложь соответственно. Последние также эквивалентны числам 1 и 0.
Как логические операторы записываются в программе Python и в чем их отличие?
Логические операторы в Python мы уже упоминали в статье «Основы программирования. Часть 2». Давайте их вспомним:

Проблема в том, что для импликации и эквиваленции нет специальных логических операторов, но для них можно использовать математические:
— Математическое сравнение на равенство работает также, как логическая эквиваленция: вернет True, если значения будут одинаковые и False в противном случае.
— Математическое “меньше или равно” полностью соответствует логическому следованию: False будет возвращено только в том случае, если значение слева будет меньше или равно значению справа. А если вспомнить аналогию логических переменных и целых чисел, это произойдет только в ситуации 1 <= 0. В остальных случаях будет истина.
Но несмотря на схожесть работы, это все еще математические операторы, из-за чего нарушается привычный приоритет. Так что в программе он будет следующим:
— Эквиваленция и импликация будут иметь равный приоритет и выполняться в порядке очереди. Но относительно логических операторов их приоритет станет самым высоким.
— Инверсия, конъюнкция и дизъюнкция будут иметь свой законный приоритет.
Самый практичный совет по записи логических уравнений в программе — не стесняйтесь использовать скобки, если используете математические операторы.
Например:
- простое логическое уравнение только из конъюнкции, дизъюнкции и инверсии в лишних скобках не нуждается (кроме тех, конечно, что уже есть в уравнении):

- при появлении импликации и эквиваленции подключаем скобки, чтобы сохранить приоритет и этих, и других логических операторов:
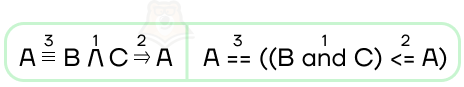
Решение практических задач
Между программированием и алгеброй логики установлен довольно приятный союз:
— С одной стороны, в больших и запутанных программах может быть много логических зависимостей, распутать которые поможет знание алгебры логики.
— С другой, не менее приятной, — программа сможет все решить за нас. Логические уравнения могут быть большими и запутанными. Законы логики помогут нам их сократить. Работать с сокращенным выражением будет проще. Но зачем упрощать, если программе достаточно будет правильно записать?
Например, очень популярная задача алгебры логики — построение таблицы истинности. Давайте попробуем предположить, что нам может понадобиться, чтобы программа смогла это сделать?
А много нам и не надо:
- Нужен перебор логических переменных по совсем небольшому диапазону — от 0 до 1.
- Правильно записанное логическое уравнение, чтобы проверить его при каждом наборе истины и лжи.
Вопрос встает только о конкретной реализации. Python — очень гибкий язык. Для разных формулировок задачи он может предложить разные инструменты, при использовании которых написание кода станет еще приятнее.
Начнем с обобщенной задачи — построение таблицы истинности. На этом примере можно показать, что математические операторы путают приоритет логических. Так что давайте составим таблицу истинности для уравнения A ≡ B ∧ C ⇒ A.
Перебор устроим с помощью вложенных циклов for. Они будут перебирать отдельные переменные, которые потом будут поставляться в логическое уравнение. Для удобства будем сохранять значение уравнения в отдельную переменную, затем выводить все на экран.
print("A B C")
for A in range(0, 2):
for B in range(0, 2):
for C in range(0, 2):
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Мы заранее подписали каждый столбец, так что не запутаться в выводе будет проще.
Да, промежуточных результатов при такой реализации у нас нет. А зачем они нам? Нам важен итоговый результат — мы его получили.
У меня есть ощущение, что этот код не очень красивый. Он однозначно рабочий, но все-таки слишком много вложенных циклов. Как это можно решить?
В статье «Комбинаторика в информатике» мы обсуждали такую вещь, как модуль itertools, который содержит функции для работы с различными комбинациями. Как раз наш случай — мы используем различные комбинации 1 и 0.
Сейчас нам пригодится функция product, которая создаст различные комбинации из указанных элементов. Изначально запишем их в отдельный массив для удобства:
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == ((B and C) <= A)
print(A, B, C, result)
Вывод:
A B C
0 0 0 False
0 0 1 False
0 1 0 False
0 1 1 True
1 0 0 True
1 0 1 True
1 1 0 True
1 1 1 True
Как видите, результат мы получили тот же, но смогли избавиться от некрасивого массива вложенных циклов. С еще большим количеством переменных в уравнении было бы нагляднее.
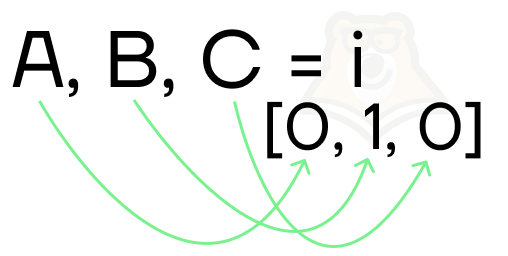
Пожалуй, стоит подробнее рассказать про строку:
A, B, C = i.
Мы точно знаем, что i — это массив с 3 элементами, так как мы изначально задали создание наборов длиной 3. Если указать перед ним ровно столько же переменных, им можно присвоить соответствующие элементы массива в одну строку.
Выше мы обсуждали, почему в этом уравнении обязательно должны быть скобки. Давайте докажем это. Построим таблицу истинности для того же уравнения, но не будем ставить скобки.
from itertools import product
print("A B C")
d = [0, 1]
for i in product(d, repeat = 3):
A, B, C = i
result = A == B and C <= A
print(A, B, C, result)
Вывод:
A B C
0 0 0 True
0 0 1 False
0 1 0 False
0 1 1 False
1 0 0 False
1 0 1 False
1 1 0 True
1 1 1 True
Не вышло: итоговые значения таблиц истинности разные. Значит, приоритет действительно нарушается.
Другая наша возможная цель — проверить, будет ли выражение истинным всегда? Получим ли мы истину при любом наборе логических переменных?
Как и в прошлый раз, у нас есть не один вариант реализации. Будем анализировать выражение А ∧ (В ∨ С) ≡ В.
Первый вариант:
- перебор всех наборов — вложенными циклами или с помощью product;
- сохранение всех результатов уравнения от каждого набора;
- проверка, чтобы ни одно значение не было ложным — для сохранения всех результатов можно использовать список.
from itertools import product
d = [0, 1]
all_results = []
for i in product(d, repeat = 3):
A, B, C = i
result = (A and (B or C)) == B
all_results.append(result)
if False not in all_results:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Вывод: Функция истинна не всегдаPython не был бы Python, если бы не дал нам возможность записать все практически в одну строку.
Второй вариант — функция all. Она возвращает True, если все значения внутри нее равны True — как раз наш случай. Чтобы записать программу максимально коротко, прямо внутри нее можно прописать и уравнение, и перебор его элементов:
from itertools import product
d = [0, 1]
result = all((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция полностью истинна")
else:
print("Функция истинна не всегда")
Здесь в переменную result записывается логическое значение True, если для всех наборов А, В, С из комбинаций d длиной 3 результат логического уравнения равен True. Если же среди всех результатов есть хоть один False — функция all даст нам False.
Для похожей задачи — чтобы не все значения уравнения были ложными — можно использовать функцию any. Синтаксис абсолютно такой же, разница есть в принципе работы. any вернет True, если среди всех переданных значений есть хоть одно истинное значение.
from itertools import product
d = [0, 1]
result = any((A and (B or C)) == B for A, B, C in product(d, repeat = 3))
if result:
print("Функция не всегда ложна")
else:
print("Функция всегда ложна")
Вывод: Функция не всегда ложна
Python — гибкий язык. Если вам важнее видеть алгоритм работы кода более явно — используйте вложенные циклы, массивы для хранения значений и будьте более, чем на 100% уверены в каждом шаге. Если же вы хотите использовать дополнительные инструменты для сокращения объема кода и, как следствие, более быстрого его написания — вам в помощь комбинации product из itertools и инструменты массовой проверки all и any.
Фактчек
- Для импликации и эквиваленции в Python используются математические операторы сравнения, что немного нарушает их общий приоритет. Сохранить его можно с помощью скобок.
- Значения истины и лжи в Python являются логическим типом данных, который может принимать значение True или False и соответствует 1 и 0.
- Функция all проверяет, все ли переданные ей значения истинны. Функция any проверяет, есть ли среди всех переданных значений хоть одно истинное.
Проверь себя
Задание 1.
Для выражения А ∨ В ∧ ¬(В ∧ А) выберите верную запись на языке Python (с сохранением порядка действий):
- A and B or not B or A
- A and B or not (B or A)
- A or B and not B and A
- A or B and not (B and A)
Задание 2.
Для выражения ¬А ⇒ В ≡ А ∧ В выберите верную запись на языке Python (с сохранением порядка действий):
- not (А <= В == А and В)
- not А <= В == (А and В)
- ((not A) <= B) == (A and B)
- (not А) <= (В == (А and В))
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения:
A ∧ B ⇒ C ∧ D ∨ D ∧ A?
- 11101101
- 11101111
- 00000011
- 11000111
Задание 4.
Выберите уравнение, которое во всех случаях принимает значение истины:
- ¬(A ∧ B) ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ ¬A)
- A ∧ B ∧ ¬(C ∧ ¬A)
- ¬(A ∧ B) ∨ ¬(C ∧ A)
Ответ: 1. — 4; 2. — 3; 3. — 1; 4. — 2.
Питон и таблицы истинности
Хотите готовиться со мной к ЕГЭ?
Пишите: ydkras@mail.ru
Немного обо мне.
Таблица истинности — это таблица, где перечисляются комбинации аргументов некой логической функции и указывается, какие значения принимает эта функция.
В задаче 2 ЕГЭ по информатике требуется 1) уметь строить таблицы истинности логического выражения и 2) уметь сравнивать построенную таблицу истинности с таблицей, приведенной в условии задачи.
Первый пункт можно выполнить на компьютере, написав несложную (менее 10 строк) программу на Питоне.
Вообще говоря, в Питоне, как и в паскале, есть специальные логические значения True и False. Но в логических выражениях можно использовать и числа. При этом значение 0 считается ложью, а всё, отличное от нуля — истиной. (Тут создатель Питона позаимствовал идею из С.)
Рассмотрим задачу с сайта «Решу ЕГЭ». В ней требуется сопоставить переменные, входящие в логическую функцию
((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y))
и таблицу
| Переменная 1 | Переменная 2 | Переменная 3 | Переменная 4 | Функция |
|---|---|---|---|---|
| ??? | ??? | ??? | ??? | F |
| 1 | — | — | 1 | 0 |
| 1 | — | — | — | 0 |
| — | 1 | — | 1 | 0 |
Требуется выяснить, какая переменная в таблице обозначена как «переменная 1», «переменная 2» и т.д.
Из последнего столбца видно, что нам нужны те комбинации значений переменных, при которых функция ложна.
Так как в Питоне отсутствует логическая операция импликации, заменяем выражения вроде x → y на эквивалентные выражения not x or y. Операция эквивалентности — это сравнение «==».
Таким образом, наша функция
((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y))
в Питоне выглядит так:
f = ((not x or y ) and (not y or w)) or (z == ( x or y))
Чтобы перебрать все возможные комбинации переменных, записываем четыре вложенных цикла вида for x in range(2): (в них переменные принимают значения 0 и 1).
Печатаем строку значений x, y, z, w тогда, когда функция f ложна (т.е. if not f:)
Вот программа, которая вычисляет таблицу истинности и печатает строки значений x, y, z и w, когда функция f имеет значение «ложь»:
for x in range(2):
for y in range(2):
for z in range(2):
for w in range(2):
f = ((not x or y ) and (not y or w)) or (z == ( x or y))
if not f: print(x,y,z,w)
Программа печатает следующую таблицу:
0 1 0 0
1 0 0 0
1 0 0 1
1 1 0 0
Столбцы слева направо — это значения переменных x, y, z, w соответственно.
Таким образом, мы очень упростили первую часть задачи — построение таблицы истинности. Осталась вторая часть.
В нашей таблице четыре строки, а в задаче — только три. Следовательно, одна строка в нашей таблице лишняя.
Заметим, что в таблице из задачи пять единиц, а в нашей таблице — шесть. Отсюда вытекают два вывода. Во-первых, мы не можем удалить из нашей таблицу строчку с двумя единицами — тогда у нас их останется четыре, т.е. менее, чем в таблице из задачи. Во-вторых, при удалении из нашей таблицы строки с одной единицей и в нашей таблице, и в таблице из задачи будет по пять единиц. Следовательно, во всех пустых клетках таблицы из задачи записаны нули.
Самую первую строку из нашей таблицы удалить нельзя: тогда у нас появляется столбец из трёх единиц, а такого столбца в таблица из задачи нет. Убираем вторую строку и получаем следующую таблицу:
0 1 0 0
1 0 0 1
1 1 0 0
В столбце переменной z — только нули. Следовательно, в задаче переменная 3 — это z.
В столбце переменной w только одна единица. Следовательно, переменная w — это переменная 2 в задаче.
Замечаем, что когда переменная w (переменная 2 в задаче) равна 1, то равна 1 также и переменная x (а в задаче это переменная 4). Следовательно, переменная 4 — это x. Оставшаяся переменная 1 — это переменная y.
Итак, наш ответ — ywzx. Именно такой ответ и приводится в задаче.
При записи логических выражений в Питоне можно столкнуться с тем, что выражения вроде (x ≡ ¬z) при буквальном их переводе (x == not z) вызывают синтаксическую ошибку. Чтобы избежать этого, надо либо заключить выражение not z в дополнительные скобки, т.е. написать (x == (not z)). Можно также заменить операцию «равно» на «не равно», т.е. записать это выражение как (x != z).
(c) Ю.Д.Красильников, 2021 г.
Дополнительные сведения, основанные на том, что я нашел здесь и там, когда искал оператор импликации: вы можете использовать хитроумный прием, чтобы определить свои собственные операторы. Вот работающий пример с аннотациями источников, которые привели меня к такому результату.
#!/usr/bin/python
# From http://code.activestate.com/recipes/384122/ (via http://stackoverflow.com/questions/932328/python-defining-my-own-operators)
class Infix:
def __init__(self, function):
self.function = function
def __ror__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __rlshift__(self, other):
return Infix(lambda x, self=self, other=other: self.function(other, x))
def __or__(self, other):
return self.function(other)
def __rshift__(self, other):
return self.function(other)
def __call__(self, value1, value2):
return self.function(value1, value2)
from itertools import product
booleans = [False,True]
# http://stackoverflow.com/questions/16405892/is-there-an-implication-logical-operator-in-python
# http://jacob.jkrall.net/lost-operator/
operators=[
(Infix(lambda p,q: False), "F"),
(Infix(lambda p,q: True), "T"),
(Infix(lambda p,q: p and q), "&"),
(Infix(lambda p,q: p or q) , "V"),
(Infix(lambda p,q: p != q) , "^"),
(Infix(lambda p,q: ((not p) or not q)), "nad"),
(Infix(lambda p,q: ((not p) and not q)), "nor"),
(Infix(lambda p,q: ((not p) or q)), "=>"),
]
for op,sym in operators:
print "nTruth tables for %s" % sym
print "nptqtp %s qtq %s p" % (sym,sym)
for p,q in product(booleans,repeat=2):
print "%dt%dt%dt%d" % (p,q,p |op| q,q |op| p)
print "nptqtrtp %s qtq %s rt(p %s q) %s rtp %s (q %s r)tp %s q %s r" % (sym,sym,sym,sym,sym,sym,sym,sym)
for p,q,r in product(booleans,repeat=3):
print "%dt%dt%dt%dt%dt%dtt%dtt%d" % (p,q,r,p |op| q,q |op| r, (p |op| q) |op| r, p |op| (q |op| r), p |op| q |op| r)
assert( (p |op| q) |op| r == p |op| q |op| r)
