- Главная
- Калькуляторы
- Математический калькулятор
Математический калькулятор
Математический-Калькулятор-Онлайн v.1.0
Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.
Решение:
Как работать с математическим калькулятором
| Клавиша | Обозначение | Пояснение |
|---|---|---|
| цифры 0-9 | Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/- | |
| точка (запятая) | Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5 | |
| знак плюс | Сложение чисел (целые, десятичные дроби) | |
| знак минус | Вычитание чисел (целые, десятичные дроби) | |
| знак деления | Деление чисел (целые, десятичные дроби) | |
| знак умножения | Умножение чисел (целые, десятичные дроби) | |
| корень | Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2 | |
| возведение в квадрат | Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16 | |
| дробь | Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число | |
| процент | Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%» | |
| открытая скобка | Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10 | |
| закрытая скобка | Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки | |
| плюс минус | Меняет знак на противоположный | |
| равно | Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат. | |
| удаление символа | Удаляет последний символ | |
| сброс | Кнопка сброса. Полностью сбрасывает калькулятор в положение «0» |
Алгоритм работы онлайн-калькулятора на примерах
Сложение.
Пример:
Сложение целых натуральных чисел { 5 + 7 = 12 }
Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }
Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }
Вычитание.
Пример:
Вычитание целых натуральных чисел { 7 — 5 = 2 }
Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }
Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }
Умножение.
Пример:
Произведение целых натуральных чисел { 3 * 7 = 21 }
Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }
Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }
Деление.
Пример:
Деление целых натуральных чисел { 27 / 3 = 9 }
Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }
Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }
Извлечение корня из числа.
Пример:
Извлечение корня из целого числа { корень(9) = 3 }
Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }
Извлечение корня из суммы чисел { корень(56 + 25) = 9 }
Извлечение корня из разницы чисел { корень (32 – 7) = 5 }
Возведение числа в квадрат.
Пример:
Возведение в квадрат целого числа { (3) 2 = 9 }
Возведение в квадрат десятичных дробей { (2,2) 2 = 4,84 }
Перевод в десятичные дроби.
Пример:
{ 1/3 = 0,33 }
{ ½ = 0,5 }
Вычисление процентов от числа
Пример:
Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }
Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }
18% от числа 140 это { 140 * 0,18 = 25,2 }
- Альфашкола
- Статьи
- Сложение и вычитание отрицательных чисел
Сложение и вычитание отрицательных чисел
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов —
положительные числа
и
отрицательные числа
. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
((-2)+(-3)=-5)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
((-8)+4=4-8=-4)
(9+(-4)=9-4=5)
Для каждого числа кроме (0) существует противоположный элемент, при сумме с ним образуется ноль:
(-9+9=0) (7,1+(-7,1)=0)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.
((-7)-(-6)=(-7)+6=(-1))
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
(7-9=-2) так как (9>7)
- Также не стоит забывать минус на минус дает плюс:
(7-(-9)=7+9=16)
- (4+(-5))
- (-36+15)
- ((-17)+(-45))
- (-9+(-1))
Решение:
- (4+(-5)=4-5=-1)
- (-36+15=-21)
- ((-17)+(-45)) (=-17-45=-62)
- (-9+(-1)=-9-1=-10)
- (3-(-6))
- (-16-35)
- (-27-(-5))
- (-94-(-61))
Решение:
- (3-(-6)=3+6=9)
- (-16-35=-51)
- (-27-(-5)=-27+5=-22)
- (-94-(-61)=-94+61=-33)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Репетитор по математике
Южно-Российский государственный политехнический университет им. М.И. Платова
Репетитор по математике
Гомельский государственный университет им. Ф. Скорины
Как решать примеры с минусами
Еще в начальной школе учат, как складывать и вычитать числа. Для того чтобы научиться это делать, необходимо выучить таблицу сложения и основанную на ней таблицу вычитания. Получается, первоклашка сможет из семнадцати вычесть девять или решить любой подобный пример. Однако завести в тупик его сможет пример обратного характера: как вычесть из девяти семнадцать. Примеры с отрицательными числами даются по школьной программе много позже, когда человек созревает до абстрактного мышления.

Инструкция
Математических действий существует четыре вида: сложение, вычитание, умножение и деление. Поэтому примеров с минусами будет четыре типа. Отрицательные числа внутри примера выделяются скобками для того, чтобы не перепутать математическое действие. Например, 6-(-7), 5+(-9), -4*(-3) или 34:(-17).
Сложение. Данное действие может иметь вид:1) 3+(-6)=3-6=-3. Замена действия: сначала раскрываются скобки, знак «+» меняется на противоположный, далее из большего (по модулю) числа «6» отнимается меньшее — «3», после чего ответу присваивается знак большего, то есть «-«.
2) -3+6=3. Этот пример можно записать по-другому («6-3») или решать по принципу «из большего отнимать меньшее и присваивать ответу знак большего».
3) -3+(-6)=-3-6=-9. При раскрытии скобок происходит замена действия сложения на вычитание, затем суммируются модули чисел и результату ставиться знак «минус».
Вычитание.1) 8-(-5)=8+5=13. Раскрываются скобки, знак действия меняется на противоположный, получается пример на сложение.
2) -9-3=-12. Элементы примера складываются и ответ получает общий знак «-«.
3) -10-(-5)=-10+5=-5. При раскрытии скобок снова меняется знак на «+», далее из большего числа отнимается меньшее и у ответа — знак большего числа.
Умножение и деление.При выполнении умножения или деления знак не влияет на само действие. При произведении или делении чисел с разными знаками ответу присваивается знак «минус», если числа с одинаковыми знаками — у результата всегда знак «плюс».1)-4*9=-36; -6:2=-3.
2)6*(-5)=-30; 45:(-5)=-9.
3)-7*(-8)=56; -44:(-11)=4.
Источники:
- таблица с минусами
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
В этом уроке мы не будем разбирать, как решаются
линейные
или
квадратные
неравенства.
Нас будет интересовать только вопрос:
«Как записать ответ неравенства специальными математическими знаками,
например, в виде
x ∈ (3; +∞) ?».
Стоит отметить, что далеко не во всех учебных заведениях требуют обязательно записывать ответ неравенства
в виде
x ∈ (3; +∞) .
В некоторых школах в 8 и 9 классе разрешают оставлять ответ, используя знаки
больше
«>» и «<». Например, следующим образом.
Ответ: x > 3
Впрочем, мы рекомендуем освоить запись ответа неравенства в математических обозначениях сразу, так как в любом случае
в старшей школе и затем в университете будут требовать именно такую запись ответа.
Перед разбором, как записывать ответ неравенства математическими знаками,
вспомним расшифровку и обозначение этих знаков.
| Знак | Расшифровка |
|---|---|
| ∈ |
«Принадлежит»
Легко запомнить знак, как зеркальное отображение русской буквы |
| ( … ) |
«Круглые скобки» Используются, когда число на границе интервала НЕ входит в сам интервал. На числовой оси такие числа обозначают «пустой» точкой. |
| [ … ] |
«Квадратные скобки» Используются, когда число на границе интервала входит в сам интервал. На числовой оси такие числа обозначают «заполненной» точкой. |
| ∪ |
«Объединение» Знак похож на подковку. Используется для объединения двух и более интервалов. |
| + ∞ |
«Плюс бесконечность» Изображается как цифра «8» на боку со знаком «+» слева. Обозначает бесконечность на положительном (правом) краю числовой оси. |
| − ∞ |
«Минус бесконечность» |
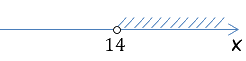
Перейдем к непосредственной записи ответа неравенства. Рассмотрим и решим линейное неравенство.
x − 6 > 8
x > 6 + 8
x > 14
Мы решили линейное неравенство, теперь запишем его ответ с помощью математических знаков.
Важно!
Перед тем, как записывать ответ неравенства, обязательно изобразите его на числовой оси.
Итак, мы изобразили ответ неравенства на числовой оси. После этого запишем слово
«Ответ:» и за ним запишем «x ∈».
Такая запись читается как «икс принадлежит».
Ответ: x ∈
Взглянув на рисунок ответа на числовой оси, мы видим, что область
решений начинается с числа «14».
Число «14» не входит в область решений («пустая» точка на оси). Значит, используем круглую скобку.
Ответ: x ∈ (14; …
Нам остается понять, где заканчивается область решений справа. Правильный ответ —
справа область заканчивается в положительной бесконечности «+ ∞».
На числовой оси на обоях краях слева и справа соответственно расположены «минус» и «плюс» бесконечности.
Как правило, их не рисуют на числовой оси лишний раз, т.к. их наличие на оси подразумевается.
Запишем окончательный ответ.
Ответ: x ∈ (14; + ∞)
Запомните!
Знаки «+ ∞»
и «− ∞» всегда записываются с
круглыми скобками.
Разберем другой пример.
−7x ≥ 56
−7x ≥ 56 | :(−7)
x ≤ 8
Также как и в предыдущем примере всегда
начинаем записывать
ответ с записи «x ∈…».
Ответ: x ∈
В ответе «x ≤ 8» область решений
начинается с «− ∞» и заканчивается на
«8», которое входит в ответ. Значит, «8» будет с
квадратной скобкой.
Так и запишем в ответе.
Ответ: x ∈ (− ∞; 8]
Запись ответа неравенства для квадратных неравенств
При решении квадратных неравенств часто может получаться несколько интервалов в ответе. Разберемся, как их записывать в ответ.
Рассмотрим пример квадратного неравенства и его решение.
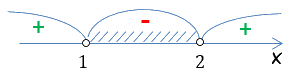
x2 − 3x + 2 < 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
1 < x < 2
В ответе мы получили один интервал. Запишем его в ответ. Как обычно, начнем запись ответа с «x ∈».
Далее используем круглые скобки, т.к. оба числа не входят в границы интервалов.
Ответ: x ∈ (1 ; 2)
Рассмотрим другой пример квадратного неравенства и его решения.
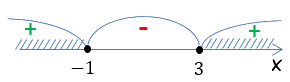
x2 − 2x − 3 ≥ 0
x1;2 =
| 2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x ≤ −1; x ≥ 3
В ответе неравенства мы получили два интервала в области решений
(x ≤ −1; x ≥ 3) и оба интервала нужно записать в ответ.
Запись ответа неравенства всегда делается слева направо (как мы привыкли читать).
Начнем слева направо записывать интервалы в ответ. Первый интервал начинается с «минус» бесконечности и заканчивается на
«−1» (включительно).
Так и запишем.
Ответ: x ∈ (− ∞; −1] …
Второй интервал начинается с «2»(включительно) и заканчивается на «плюс» бесконечности.
Для объединения интервалов используем знак «∪» («объединение»).
Ответ: x ∈ (− ∞; −1] ∪ [3 ; + ∞)