Косинус в квадрате и синус в квадрате
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
ОПРЕДЕЛЕНИЕ
Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2
| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом: и Тогда Полученное выражение представляет собой правую часть формулы произведения синусов, т.е. |
| Ответ | 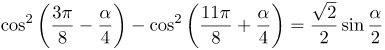 |
| Понравился сайт? Расскажи друзьям! | |
Лучший ответ
yellow submarine
Гуру
(4351)
10 лет назад
будет 1, это основное тригонометрическое тождество
Aftor
Гуру
(3830)
10 лет назад
Единица
Это основное тригонометрическое тождество
Дивергент
Высший разум
(1456952)
10 лет назад
Единица. Это называется основное тригонометрическое тождество. Вытекает из теоремы Пифагора.
Damir Б
Знаток
(251)
10 лет назад
равно единице
Юлия
Знаток
(278)
6 лет назад
1
Иван Гладких
Ученик
(210)
3 года назад
Но ведь не равно единице)) То, что вытекает из теоремы Пифагора не значит, что равно единице. Учите математику и будет вам счастье
Хотя.. . хотя никогда на множестве действительных чисел.
sin(a)*cos(a) = 1/2 * 2*sin(a)*cos(a) = 1/2 * sin(2a)
При a из Re это принимает значения от -1/2 до +1/2.
Но если взять комплексные значения а, то можно получить любое значение. В т. ч. и 1.
В общем случае (т. е. как тождество) — конечно же нет!
Вопрос:
косинус в квадрате альфа делить на синус aльфа плюс один
К сожалению, ответа на данный вопрос пока нет.
Похожие вопросы
-
В двух комнатах 45 чел. Из первой вышли 9, а из второй-14, и людей в комнатах стало поро вну .Сколько человек было в комнатах сначала?
-
Мальчик купил тетрадь на казахском
-
( с , сс )ориться
Как писать?????
-
пожалуйста очень срочно надо помогитееееее
-
Лодка шла по озеру со скоростью 8,5 км/ч в течение 3,5 ч, а затем 2,5 вниз по реке.Какое расстояние прошла лодка, если её скорость не менялась , а скорость течения реки составляла 1,3 км/ч?
РЕШИТЬ УРАВНЕНИЕМ
-
напишите что такое гермафродиты и мини сочинение на тему пиявки токо не из интернета
-
что из перечисленного ниже относится к переменным издержкам? 1)зарплата аппарата управления 2)стоимость охраны помещения 3) плата за электроэнергию 4) страховые взносы
-
может ли в плановой экономике действовать закон спроса и предложения на труд
-
Помагите пожалуйста выполнять задания
-
Что такое коэффициент увлажнения В каких районах нашей страны к 1 в каких комиссио нного и почему
Помощь с домашними заданиями. Решение задач, ответы на вопросы учеников и студентов.
OTVETYTUT.COM — 2018
Главная
Контакты
Содержание
- Косинус в квадрате, синус в квадрате
- Основные тождества тригонометрии
- Формулы приведения
- Тригонометрические формулы сложения
- Формулы кратного угла: двойного, тройного и т.д.
- Формулы половинного угла
- Формулы понижения степени
- Сумма и разность тригонометрических функций
- Произведение тригонометрических функций
- Универсальная тригонометрическая подстановка
‘);> //—>
Косинус (cos) — это тригонометрическая функция, геометрически представляющая отношение прилежащего катета к гипотенузе в прямоугольном треугольнике.
cos 2 (x)=cos(x)*cos(x)
Значение косинуса находится в диапазоне от -1 до +1.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор вычисления квадрата косинуса (косинуса в квадрате). С помощью этого калькулятора вы в один клик сможете вычислить квадрат косинус любого угла.
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение икс — «x», что не меняет сути).
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin 2 α + cos 2 α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin 2 α = 1 — cos 2 α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin 2 α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos 2 α = 1 — sin 2 α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos 2 α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Редактировать этот урок и/или добавить задание и получать деньги постоянно* Добавить свой урок и/или задания и получать деньги постоянно
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
user->isGuest) < echo (Html::a(‘Войдите’, [‘/user/security/login’], [‘class’ =>»]) . ‘ или ‘ . Html::a(‘зарегистрируйтесь’, [‘/user/registration/register’], [‘class’ => »]) . ‘ , чтобы получать деньги $$$ за каждый набранный балл!’); > else < if(!empty(Yii::$app->user->identity->profile->first_name) || !empty(Yii::$app->user->identity->profile->surname))< $name = Yii::$app->user->identity->profile->first_name . ‘ ‘ . Yii::$app->user->identity->profile->surname; > else < $name = »; >echo ‘Получайте деньги за каждый набранный балл!’; > ?>—>
При правильном ответе Вы получите 8 баллов
Упростить выражение с квадратом косинуса:
Выберите всего один правильный ответ.
Добавление комментариев доступно только зарегистрированным пользователям
Lorem iorLorem ipsum dolor sit amet, sed do eiusmod tempbore et dolore maLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborgna aliquoLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempbore et dLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborlore m mollit anim id est laborum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Lorem ipsum dolor sit amet, consectetu sed do eiusmod qui officia deserunt mollit anim id est laborum.
28.01.17 / 22:14, Иван ИвановичОтветить -2
Lorem ipsum dolor sit amet, consectetur adipisicing sed do eiusmod tempboLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod temLorem ipsum dolor sit amet, consectetur adipisicing elit, sed do eiusmod tempborpborrum.
28.01.17 / 22:14, Иван Иванович Ответить +5
Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
sin 2 a + cos 2 a = 1 t g α = sin α cos α , c t g α = cos α sin α t g α · c t g α = 1 t g 2 α + 1 = 1 cos 2 α , c t g 2 α + 1 = 1 sin 2 α
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
sin α + 2 π z = sin α , cos α + 2 π z = cos α t g α + 2 π z = t g α , c t g α + 2 π z = c t g α sin — α + 2 π z = — sin α , cos — α + 2 π z = cos α t g — α + 2 π z = — t g α , c t g — α + 2 π z = — c t g α sin π 2 + α + 2 π z = cos α , cos π 2 + α + 2 π z = — sin α t g π 2 + α + 2 π z = — c t g α , c t g π 2 + α + 2 π z = — t g α sin π 2 — α + 2 π z = cos α , cos π 2 — α + 2 π z = sin α t g π 2 — α + 2 π z = c t g α , c t g π 2 — α + 2 π z = t g α sin π + α + 2 π z = — sin α , cos π + α + 2 π z = — cos α t g π + α + 2 π z = t g α , c t g π + α + 2 π z = c t g α sin π — α + 2 π z = sin α , cos π — α + 2 π z = — cos α t g π — α + 2 π z = — t g α , c t g π — α + 2 π z = — c t g α sin 3 π 2 + α + 2 π z = — cos α , cos 3 π 2 + α + 2 π z = sin α t g 3 π 2 + α + 2 π z = — c t g α , c t g 3 π 2 + α + 2 π z = — t g α sin 3 π 2 — α + 2 π z = — cos α , cos 3 π 2 — α + 2 π z = — sin α t g 3 π 2 — α + 2 π z = c t g α , c t g 3 π 2 — α + 2 π z = t g α
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
sin α ± β = sin α · cos β ± cos α · sin β cos α + β = cos α · cos β — sin α · sin β cos α — β = cos α · cos β + sin α · sin β t g α ± β = t g α ± t g β 1 ± t g α · t g β c t g α ± β = — 1 ± c t g α · c t g β c t g α ± c t g β
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 sin 2 α , cos 2 α = 2 cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α с t g 2 α = с t g 2 α — 1 2 · с t g α sin 3 α = 3 sin α · cos 2 α — sin 3 α , sin 3 α = 3 sin α — 4 sin 3 α cos 3 α = cos 3 α — 3 sin 2 α · cos α , cos 3 α = — 3 cos α + 4 cos 3 α t g 3 α = 3 t g α — t g 3 α 1 — 3 t g 2 α c t g 3 α = c t g 3 α — 3 c t g α 3 c t g 2 α — 1
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
sin 2 α 2 = 1 — cos α 2 cos 2 α 2 = 1 + cos α 2 t g 2 α 2 = 1 — cos α 1 + cos α c t g 2 α 2 = 1 + cos α 1 — cos α
Формулы понижения степени
sin 2 α = 1 — cos 2 α 2 cos 2 α = 1 + cos 2 α 2 sin 3 α = 3 sin α — sin 3 α 4 cos 3 α = 3 cos α + cos 3 α 4 sin 4 α = 3 — 4 cos 2 α + cos 4 α 8 cos 4 α = 3 + 4 cos 2 α + cos 4 α 8
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
sin n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 ( — 1 ) n 2 — k · C k n · cos ( ( n — 2 k ) α ) cos n α = C n 2 n 2 n + 1 2 n — 1 ∑ k = 0 n 2 — 1 C k n · cos ( ( n — 2 k ) α )
sin n α = 1 2 n — 1 ∑ k = 0 n — 1 2 ( — 1 ) n — 1 2 — k · C k n · sin ( ( n — 2 k ) α ) cos n α = 1 2 n — 1 ∑ k = 0 n — 1 2 C k n · cos ( ( n — 2 k ) α )
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
sin α + sin β = 2 sin α + β 2 · cos α — β 2 sin α — sin β = 2 sin α — β 2 · cos α + β 2 cos α + cos β = 2 cos α + β 2 · cos α — β 2 cos α — cos β = — 2 sin α + β 2 · sin α — β 2 , cos α — cos β = 2 sin α + β 2 · sin β — α 2
Произведение тригонометрических функций
Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.
Формулы произведения тригонометрических функций
sin α · sin β = 1 2 · ( cos ( α — β ) — cos ( α + β ) ) cos α · cos β = 1 2 · ( cos ( α — β ) + cos ( α + β ) ) sin α · cos β = 1 2 · ( sin ( α — β ) + sin ( α + β ) )
Универсальная тригонометрическая подстановка
Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.
Универсальная тригонометрическая подстановка
sin α = 2 t g α 2 1 + t g 2 α 2 cos α = 1 — t g 2 α 2 1 + t g 2 α 2 t g α = 2 t g α 2 1 — t g 2 α 2 c t g α = 1 — t g 2 α 2 2 t g α 2
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
Все формулы по тригонометрии
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$
$$tgx= frac{sinx}{cosx}$$
$$ctgx= frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= frac{1}{cos^2x}$$
$$ctg^2x+1= frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$
begin{align}
sin2x &=frac{2tgx}{1+tg^2x}\
&= frac{2ctgx}{1+ctg^2x}\
&= frac{2}{tgx+ctgx}
end{align}
begin{align}
cos2x & = cos^2x-sin^2x\
&= 2cos^2x-1\
&= 1-2sin^2x
end{align}
begin{align}
cos2x & = frac{1-tg^2x}{1+tg^2x}\
&= frac{ctg^2x-1}{ctg^2x+1}\
&= frac{ctgx-tgx}{ctgx+tgx}
end{align}
begin{align}
tg2x & = frac{2tgx}{1-tg^2x}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{2}{ctgx-tgx}
end{align}
begin{align}
ctg2x & = frac{ctg^2x-1}{2ctgx}\
&= frac{2ctgx}{ctg^2x-1}\
&= frac{ctgx-tgx}{2}
end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$
$$cos3x=4cos^3x-3cosx$$
$$tg3x= frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
begin{align}
tg frac{x}{2} & = frac{1-cosx}{sinx}\
&= frac{sinx}{1+cosx}
end{align}
begin{align}
ctg frac{x}{2} & = frac{1+cosx}{sinx}\
&= frac{sinx}{1-cosx}
end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= frac{1-cos2x}{2}$$
$$cos^2x= frac{1+cos2x}{2}$$
$$tg^2x= frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= frac{1+cos2x}{1-cos2x}$$
$$sin^2 frac{x}{2}= frac{1-cosx}{2}$$
$$cos^2 frac{x}{2}= frac{1+cosx}{2}$$
$$tg^2 frac{x}{2}= frac{1-cosx}{1+cosx}$$
$$ctg^2 frac{x}{2}= frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= frac{3sinx-sin3x}{4}$$
$$cos^3x= frac{3cosx+cos3x}{4}$$
$$tg^3x= frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= frac{3-4cos2x+cos4x}{8}$$
$$cos^4x= frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(alpha + beta) = sin alpha cos beta + cos alpha sin beta$$
$$cos(alpha + beta) = cos alpha cos beta — sin alpha sin beta$$
$$tg(alpha + beta)= frac{tg alpha + tg beta}{1 — tg alpha tg beta}$$
$$ctg(alpha + beta)= frac{ctg alpha ctg beta -1}{ctg alpha + ctg beta}$$
$$sin(alpha — beta) = sin alpha cos beta — cos alpha sin beta$$
$$cos(alpha — beta) = cos alpha cos beta + sin alpha sin beta$$
$$tg(alpha — beta)= frac{tg alpha — tg beta}{1 + tg alpha tg beta}$$
$$ctg(alpha — beta)= frac{ctg alpha ctg beta +1}{ctg alpha — ctg beta}$$
Формулы суммы тригонометрических функций
$$sinalpha + sinbeta = 2sin frac{alpha + beta }{2} cdot cos frac{alpha — beta }{2}$$
$$cosalpha + cosbeta = 2cos frac{alpha + beta }{2} cdot cos frac{alpha — beta }{2}$$
$$tgalpha + tgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$ctgalpha + ctgbeta = frac{sin(alpha + beta) }{cos alpha cos beta}$$
$$(sinalpha + cosalpha)^2= 1+sin2alpha$$
Формулы разности тригонометрических функций
$$sinalpha — sinbeta = 2sin frac{alpha — beta }{2} cdot cos frac{alpha + beta }{2}$$
$$cosalpha — cosbeta = -2sin frac{alpha + beta }{2} cdot sin frac{alpha — beta }{2}$$
$$tgalpha — tgbeta = frac{sin(alpha — beta) }{cos alpha cos beta}$$
$$ctgalpha — ctgbeta = — frac{sin(alpha — beta) }{sin alpha sin beta}$$
$$(sinalpha + cosalpha)^2= 1-sin2alpha$$
Формулы произведения тригонометрических функций
$$sinalpha cdot sinbeta = frac{cos(alpha — beta)-cos(alpha + beta)}{2}$$
$$sinalpha cdot cosbeta = frac{sin(alpha — beta)+sin(alpha + beta)}{2}$$
$$cosalpha cdot cosbeta = frac{cos(alpha — beta)+cos(alpha + beta)}{2}$$
begin{align}
tgalpha cdot tgbeta & = frac{cos(alpha — beta)-cos(alpha + beta)}{cos(alpha — beta)+cos(alpha + beta)}\
&= frac{tgalpha + tgbeta}{ctgalpha + ctgbeta}
end{align}
begin{align}
ctgalpha cdot ctgbeta & = frac{cos(alpha — beta)+cos(alpha + beta)}{cos(alpha — beta)-cos(alpha + beta)}\
&= frac{ctgalpha + ctgbeta}{tgalpha + tgbeta}
end{align}
$$tgalpha cdot ctgbeta = frac{sin(alpha — beta)+sin(alpha + beta)}{sin(alpha + beta)-sin(alpha — beta)}$$



