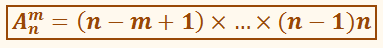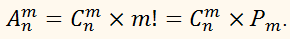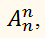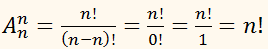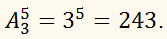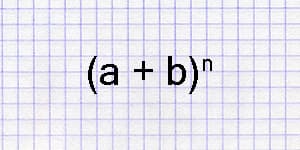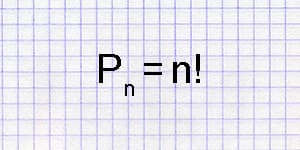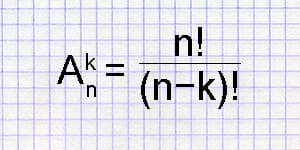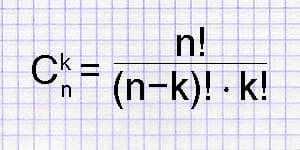ВИДЕО УРОК
Размещения.
Пусть имеется n различных объектов. Будем выбирать из
них m объектов и
переставлять всеми возможными способами между собой (то есть меняется и состав
выбранных объектов, и их порядок). Получившиеся комбинации называются
размещениями из n объектов по m.
Если
в размещении переставить местами элементы, то получится другое размещение.
Размещениями называют различные комбинации из m объектов, которые выбраны из множества n различных объектов, и которые отличаются друг
от друга как составом объектов в выборке, так и их порядком.
Количество
размещений рассчитывается по формуле:
Или
Размещениями из n элементов по
m (мест) называются такие выборки, которые имея
по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо
составом элементов, либо порядком их расположения.
Число размещений
из n по m обозначается
и определяется по
формуле
Если
вы уже знакомы с сочетаниями, то легко заметить, что чтобы найти размещения,
надо взять все возможные сочетания, а потом в каждом ещё поменять порядок всеми
возможными способами (то есть фактически сделать ещё перестановки). Поэтому
число размещений ещё выражается через число сочетаний так:
Получилась такая формула, объединяющая три формулы
комбинаторики (три концепции: размещений, сочетаний и перестановок).
Вычислим
т. е. число
размещений из n по n.
Таким образом:
Ничего
удивительного в том, что число размещений из
n по n оказалось равным
числу перестановок n элементов, так
как мы использовали для составления размещений всё множество элементов, а
значит, они уже не могут отличаться друг от друга составом элементов, только
порядком их расположения, а это и есть перестановки.
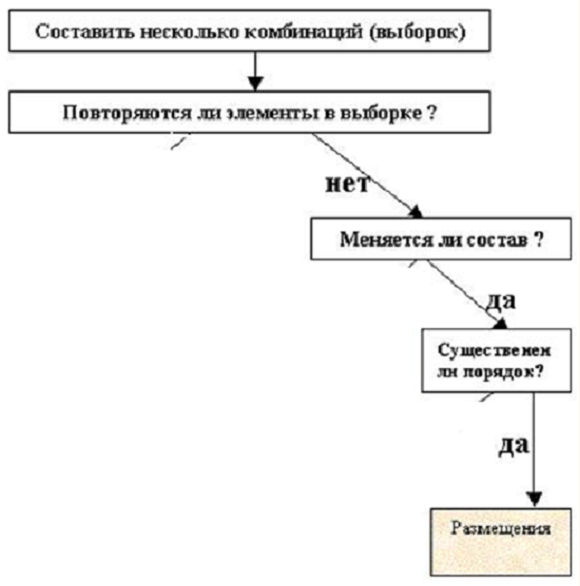
Схема для решения комбинаторных
задач на размещения.
Перед решением задачи на вычисление этого вида сочетаний
предлагается схема способствующая правильному выявлению вида сочетания согласно
условию задачи. При этом учитываются характеристические свойства каждого вида
сочетаний.
Как видно из схемы,
выбор формулы зависит от того, будут ли все элементы использоваться в
формировании сочетаний или нет, и важен ли их порядок. Применяя такую схему,
всегда можно проанализировать условие задачи и ответить на эти два главных
вопроса.
Размещения
из n элементов по 2.
Число
всех выборов двух элементов из n с учётом их
порядка, называется числом их размещений из
n элементов по
2.
Пример всех
размещений из n =
3 объектов (различных фруктов) в группы по m = 2 с учётом порядка – на картинке.
Согласно формуле,
их должно быть равно:
Число
всех выборов m элементов из n данных с учётом их порядка называют числом
размещений из n элементов по m.
ЗАДАЧА:
В студенческой группе
23 человека.
Сколькими способами можно выбрать старосту и его заместителя ?
РЕШЕНИЕ:
ОТВЕТ: 506.
Размещения с повторениями.
Классической
задачей комбинаторики является задача о числе размещений с повторениями,
содержание которой можно выразить вопросом:
Сколькими способами можно выбрать и разместить
по m различным местам m из n предметов, среди которых есть одинаковые ?
Или по другому:
Из множества, состоящего из n элементов, выбирается m элементов, при этом важен порядок элементов в
каждой выборке.
Формула количества
размещений с повторениями:
Схема для решения комбинаторных
задач на размещения с повторениями.
Перед решением задачи на вычисление этого вида сочетаний
предлагается схема способствующая правильному выявлению вида сочетания согласно
условию задачи. При этом учитываются характеристические свойства каждого вида
сочетаний.
Как видно из схемы,
выбор формулы зависит от того, будут ли все элементы использоваться в
формировании сочетаний или нет, и важен ли их порядок. Применяя такую схему,
всегда можно проанализировать условие задачи и ответить на эти два главных
вопроса.
ЗАДАЧА:
У мальчика осталось от набора для настольной игры штампы
с цифрами 1,
3 и 7.
Он решил с помощью этх штампов нанести на все книги пятизначные номера –
составить каталог. Сколько различных пятизначных номеров может составить
мальчик ?
РЕШЕНИЕ:
Можно считать, что опыт состоит в 5-кратном
выборе с возвращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров
определяется числом размещений с повторениями из 3 элементов по
5.
ОТВЕТ: 243.
ЗАДАЧА:
Сколько существует четырёхзначных пин-кодов ?
РЕШЕНИЕ:
По условию предложен набор из n =
10 цифр, из которого выбираются m =
4 цифры и располагаются в определённом
порядке, при этом цифры в выборке могут повторяться (т. е. любой цифрой
исходного набора можно пользоваться произвольное количество раз). По формуле
количества размещений с повторениями:
ОТВЕТ: 10000.
ЗАДАЧА:
Согласно государственному стандарту, автомобильный
номерной знак состоит из 3 цифр и
3 букв. При этом
недопустим номер с тремя нулями, а буквы выбираются из набора
А, В, Е, К, М, Н,
О, Р, С, Т, У, Х.
(используются только те буквы кириллицы,
написание которых совпадает с латинскими буквами). Сколько различных номерных знаков можно составить для региона ?
РЕШЕНИЕ:
способами можно составить цифровую комбинацию
автомобильного номера, при этом одну из них (000) следует исключить:
способами можно составить буквенную комбинацию
автомобильного номера.
По правилу умножения комбинаций, всего можно составить
автомобильных номера.
(каждая цифровая комбинация сочетается с
каждой буквенной комбинацией)
ОТВЕТ: 1726272.
Размещения в теории
вероятностей.
В теории
вероятностей задачи на размещения встречаются несколько реже, чем задачи на
другие типы выборок, поскольку размещения имеют больше опознавательных
признаков – и порядок, и состав элементов, а значит меньше подвержены случайному
выбору.
ЗАДАЧА:
На книжной полке находится собрание сочинений одного
автора в 6 томах. Книги одинакового формата расположены
в произвольном порядке. Читатель не глядя, берёт 3 книги. Какова вероятность того, что он взял
первые три тома ?
РЕШЕНИЕ:
Событие А –
у читателя первые три тома. С учётом порядка выбора он мог взять их 6-ю способами. (Это перестановки
из 3-ёх элементов
Р3 =
3! = 1×2×3 = 6,
которые легко перечислить
123, 132, 213, 231, 312, 321).
Таким образом, число благоприятствующих элементарных событий равно 6.
Общее число возможных элементарных событий равно числу размещений из 6-ти по 3,
т. е.
ОТВЕТ: 0,05.
Задания к уроку 4
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Простые методы решения комбинаторных задач
- Урок 2. Правила сложения и умножения
- Урок 3. Перестановки
- Урок 5. Сочетания
|
Умения |
Алгоритм |
|
Подсчет |
1. Вычисляется
2. Вычисляется 3. |
Задание
2. Биатлонист, стреляет в круг радиуса
R=2
см. В этот круг биатлонист попадает с
вероятностью 1. Попадание в любую точку
круга равновероятно. Внутри круга
радиуса R=2
см находится круг радиуса R=1
см. Если биатлонист не попадает в меньший
круг, он будет обязан бежать штрафной
круг. Какова вероятность. Что биатлонист
не побежит штрафной круг.
Решение
|
№ п/п |
Алгоритм |
Конкретное |
|
1 |
Вычислить |
Площадь |
|
2 |
Вычислить |
Площадь |
|
3 |
Разделить |
|
3. Вероятности, связанные с подсчетом числа перестановок:
|
Умения |
Алгоритм |
|
Вероятности, |
1. Подсчитывается
2. Подсчитывается 3. |
Задание
3. Имеется собрание сочинений из 6 томов
некого автора. Все 6 томов расставляются
на книжной полке случайным образом.
Какова вероятность того, что тома
распложаться в порядке 1,2,3,4,5,6 или
6,5,4,3,2,1?
Решение
|
№ п/п |
Алгоритм |
Конкретное |
|
1 |
Вычислить |
Количество |
|
2 |
Вычислить |
Количество |
|
3 |
Разделить |
|
4. Вероятности, связанные с подсчетом числа размещений: .
|
Умения |
Алгоритм |
|
Вероятности, |
1. Подсчитывается
2. Подсчитывается 3. |
Задание
4. Имеется собрание сочинений из 6 томов
некоего автора. На верхней полке умещаются
только 4 тома. Эти 4 тома берут из 6 томов
случайным образом и расставляют на
верхней полке случайным порядком. Какова
вероятность того, что тома расположатся
в порядке 1,2,3,4 или 4,3,2,1?
Решение
|
№ п/п |
Алгоритм |
Конкретное |
|
1 |
Вычислить |
Количество
|
|
2 |
Вычислить |
Количество |
|
3 |
Разделить |
|
5. Вероятности, связанные с подсчетом числа сочетаний:
|
Умения |
Алгоритм |
|
Вероятности, |
1. Подсчитывается
2. Подсчитывается 3. |
Задание
5. Имеется собрание сочинений из 6 томов
некоего автора. На верхней полке умещаются
только 4 тома. Эти 4 тома берут из 6 томов
случайным образом и расставляют на
верхней полке. Какова вероятность того,
что для размещения на верхней полке
будут выбраны тома 1,2,3,4?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Элементы комбинаторики в задачах по теории вероятности
Выполнила учитель математики
МБОУ Большемурашкинская СШ Козлова Е.Е.
Применение перестановок
Задача 1 .
На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом?
- — общее количество вариантов расстановки 30 книг;
- — количество вариантов, когда 1-й и 2-й тома стоят рядом и первый слева;
- — количество вариантов, когда первый и второй тома стоят рядом
- -всего вариантов нужного размещения
Применение перестановок
Задача 2.
На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом?
- — всего вариантов размещения;
- — количество вариантов, когда первый и второй тома стоят рядом;
- — вероятность, что первый и второй тома будут стоять рядом;
- — вероятность, что первый и второй тома не будут стоять рядом.
Применение размещений
Задача 3.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг?
Задача 4.
Сколькими способами можно расставить 30 книг на двух полках, если на каждой из них помещается только по 15 томов?
Применение размещений
Задача 5.
На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинакового формата расположены в произвольном порядке. Читатель, не глядя, берет 3 книги. Какова вероятность того, что он взял первые три тома?
Применение сочетаний
Задача 6.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 30-ти книг?
Задача 7.
Сколькими способами можно расставить 30 внешне неразличимых книг на двух полках, если на каждой из них помещается только по 15 томов?
Применение сочетаний
Задача 8.
На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинаково оформлены и расположены в произвольном порядке. Читатель берет наугад 3 книги. Какова вероятность того, что он взял первые три тома?
Пример 1. Выписать все перестановки и найти их число для множества М= состоящего из 5 элементов.
Данный калькулятор находит все перестановки элементов множества заданных и буквами, и числами, можно и вперемешку.
Пример 2. Дано число элементов n. Найти число перестановок можно по формуле
Пример 3. Сколько различных четырехзначных чисел можно составить из цифр 0, 1, 2, 3, если каждая цифра в изображении числа встречается один раз?
Решение. Рассматриваемое число может быть представлено как некоторая перестановка из цифр 0, 1, 2, 3, в которой первая цифра отлична от нуля. Так как число перестановок из четырех цифр равна P4=4! и из них 3! перестановок начинаются с нуля, то искомое количество равно
4! – 3! = 3×3! = 3×1×2×3 = 18.
Задачи.
1.21. Пассажирский поезд состоит из трех багажных вагонов и восьми купированных. Сколькими способами можно сформировать состав, если багажные вагоны должны находится в его начале?
1.22. Четыре мальчика и четыре девочки рассаживаются в ряд на восемь подряд расположенных мест, причем мальчики садятся на четные места, а девочки – на нечетные. Сколькими способами они могут это сделать?
1.23. Сколькими способами можно посадить за круглый стол трех мужчин и трех женщин так, чтобы никакие два лица одного пола не сидели рядом?
1.24. На собрании должны выступить 5 человек: А, Б, В, Г, Д. Сколькими способами можно расположить их в списке ораторов, если Б не должен выступать до того, как выступил А? Решите эту же задачу, если Б должен выступить сразу после А.
Источник
Комбинаторика
Комбинаторика онлайн калькуляторы
| Элементы комбинаторики перестановки, размещения, сочетания |
Число перестановок находит все варианты перестановки |
| Обратная перестановка онлайн калькулятор |
Количество инверсий в перестановке это количество пар элементов |
| Циклическая перестановка перевод цикла в стандарт |
Число сочетаний вычисление числа сочетаний из n по k элементов |
| Порядок перестановки стандартной и циклической |
Число сочетаний с повторениями онлайн калькулятор для нахождения сочетаний |
| Число размещений нахождение количества размещений |
Разложение Бинома Ньютона калькулятор разложения степени |
| Комбинаторные уравнения решение комбинаторных уравнений |
Смотрите также
Сколько существует трёхзначных чисел, которые делятся на 5?
Подскажите что использовать, перестановки с повторениями? Есть восемь элементов у каждого элемента может быть два состояния. Сколько может быть комбинаций?
составьте всевозможные перестановки из элементов множества А, если а=,иллюстрируйте решение, используя понятие регулярного дерева
У Васи есть кубики трех цветов. Он строит из них башню, ставя каждый следующий кубик на предыдущий. Запрещено использовать более 7 кубиков каждого из цветов. Вася заканчивает строить башню, как только в ней окажется по 7 кубиков каких-то двух цветов. Сколько различных башен может построить Вася?
Сколько существует четырехзначных чисел, в запись которых входит ровно одна цифра 3?
Рассмотрим четыре случая:
1) Когда число начинается на 3.
Каждый разряд (сотен, десятков и единиц) можно выбрать девятью способами.
9 × 9 × 9 = 729 чисел.
2) Когда цифра 3 в разряде сотен.
Первую цифру можем выбрать восемью способами, а третью и четвертую – девятью способами, получаем.
8 × 9 × 9 = 648 чисел.
3) Когда цифра 3 в разряде десяток.
8 × 9 × 9 = 648 чисел.
4) Когда цифра 3 в разряде единиц.
8 × 9 × 9 = 648 чисел.
Общее количество: 729 + 648 + 648 + 648 = 2673 чисел.
Источник
Элементы комбинаторики. Перестановки, размещения, сочетания
Подсчет числа перестановок, размещений и сочетаний.
Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.
Элементы комбинаторики. Перестановки, размещения, сочетания
Итак, есть множество из n элементов.
Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА
Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m
Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ
Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:
Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC
Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m
Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ
Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:
Источник
Формулы комбинаторики.
Перестановки. Подсчет числа перестановок.
Представьте себе, что вы избрали профессию, которая, казалось бы, ни каким образом не связана с математикой, например, дизайнер интерьеров. Представьте себе, что заказчик высказал вам просьбу:
Например, сначала оставляем на первом месте бордовый том, рядом с ним может находиться зеленый или оранжевый. Если на втором месте стоит зеленый том, то далее могут стоять либо оранжевый и синий, либо синий и оранжевый. Если на втором месте стоит оранжевый том, то далее могут стоять либо зеленый и синий, либо синий и зеленый. Итого, получается 4 возможных варианта.
На первом месте может стоять любой из 4-ёх томов, значит описанную процедуру надо повторить еще 3 раза. Случай, когда на первом месте стоит синий том, получается такими же рассуждениями.

В результате у нас получилось всего 12 вариантов расстановки 4-ёх книг на полке с заданным ограничением. Много это или мало? Если потратить по одной минуте на перемещение книг и обсуждение получившегося варианта с заказчиком, то, пожалуй, нормально. 12 минут можно и книжки подвигать, и поговорить. (Попробуйте посчитать, сколько получилось бы перестановок 4-ёх книг без всяких ограничений?)
А теперь представьте себе, что у заказчика книг больше, чем 4. Ну хотя бы 5. Понятно, что и вариантов расстановки будет больше, и реально переставлять их с места на место дольше, и запутаться и начать повторяться легче. Значит бросаться в бой без подготовки уже не стоит. Нужно сначала запланировать варианты на бумаге. Для краткости занумеруем наши цветные тома и будем переставлять на бумаге их номера. Чтобы меньше ошибаться, сначала выпишем все варианты перестановки, а затем вычеркнем те из них, которые подпадают под ограничение. Итак:
У нас 5 книг (или 5 цифр), каждая из которых может стоять на первом месте. Сделаем для каждого из этих 5-ти случаев свою табличку. На втором месте может стоять любая из оставшихся 4-ёх цифр, для каждой из них зарезервируем столбик в табличке.





В каждом столбике помещаем пары строк, в которых на третьем месте стоит одна из оставшихся 3-ёх цифр, а две последние цифры меняются местами. Таким образом мы аккуратно выписываем все варианты перестановок. Подсчитаем их общее число.
5(таблиц)×4(столбика)×3(пары строк)×2(строки)×1(вариант) = 120 (вариантов).
И, наконец, вычеркнем из всех таблиц варианты, содержащие «12» или «21». Таких оказалось по 6 в первой и второй табличках и по 12 в оставшихся 3-ёх, всего 48 вариантов, не удовлетворяющих ограничению. Значит заказчику надо показать 120 − 48 = 72 варианта расположения 5-ти книг. На это уйдет больше часа, даже если тратить на обсуждение каждого варианта только минуту.
Только где вы видели человека, который для перестановки пяти книг станет нанимать дизайнера? Реально такие задачи возникают в библиотеках, где нужно расставить книги для удобства посетителей, в больших книжных магазинах, где нужно расставить книги так, чтобы обеспечить увеличение спроса, и т.п. То есть там, где книг не единицы, и даже не десятки, а сотни и тысячи.
Считать варианты перестановок приходится не только для книг. Это может потребоваться для большого числа любых объектов практически в любой сфере деятельности. Значит, как дизайнерам, так и людям других профессий может понадобиться помощник, а еще лучше инструмент для облегчения подготовительного этапа, анализа возможных результатов и сокращения объема непроизводительного труда. Такие инструменты создавали и создают ученые-математики, а затем отдают их обществу в виде готовых формул. Математики не обошли своим вниманием вопросы, связанные с перестановками, а также с размещениями и сочетаниями разных элементов. Соответствующим формулам уже не один век. Эти формулы очень просты, подрастающей части общества их «вручают» на уроках школьной математики. Поэтому всё, что было написано выше, это по-существу, «изобретение велосипеда», к которому пришлось прибегнуть из-за предположения, что дизайнеру интерьеров никогда не понадобится математика. Что ж, откажемся от этого предположения. Повторим математические понятия, а затем снова вернемся к задаче о книжной полке.
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества. Составляя комбинации, мы фактически выбираем из этого множества различные элементы и объединяем их в группы по нашим потребностям, поэтому вместо слова «комбинации», часто используют слово «выборки» элементов.
Формула для числа перестановок.
Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов, но не самими элементами.
Если перестановки производятся на множестве из n элементов, их число определяется по формуле
Pn = n·(n−1)·(n−2). 3·2·1 = n!
Таким образом, общее число перестановок 5-ти книг P5 = 5! = 1·2·3·4·5 = 120, что мы и получили выше. Фактически мы выводили эту формулу для маленького примера. Теперь решим пример побольше.
Задача 1.
На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом 1-й и 2-й тома не стояли рядом?
Решение.
Это очень большое число (после двойки еще 32 цифры). Даже если затратить секунду на каждую перестановку, то потребуются миллиарды лет. Стоит ли выполнять такое требование заказчика, или лучше уметь обоснованно возразить ему и настоять на применении дополнительных ограничений?
Перестановки и теория вероятностей.
Еще чаще необходимость подсчёта числа вариантов возникает в теории вероятностей. Продолжим книжную тему следующей задачей.
Задача 2.
На книжной полке стояло 30 томов. Ребенок уронил книги с полки, а затем расставил их в случайном порядке. Какова вероятность того, что он не поставил 1-й и 2-й тома рядом?
Решение.
Замечаниe: Если непонятно, как сокращаются дроби с факториалами, то вспомните, что факториал это краткая запись произведения. Её всегда можно расписать длинно и зачеркнуть повторяющиеся множители в числителе и в знаменателе.
В ответе получилось число близкое к единице, это означает, что при таком количестве книг случайно поставить два заданных тома рядом сложнее, чем не поставить.
Размещения. Подсчет числа размещений.
Теперь предположим, что у заказчика много книг и невозможно разместить их все на открытых полках. Его просьба состоит в том, что нужно выбрать определенное количество каких-либо книг и разместить их красиво. Красиво получилось или некрасиво это вопрос вкуса заказчика, т.е. он опять хочет посмотреть все варианты и принять решение сам. Наша задача состоит в том, чтобы посчитать количество всех возможных вариантов размещения книг, обоснованно переубедить его и ввести разумные ограничения.
На рисунке представлены только 4 варианта размещения из 60 возможных. Сравните картинки. Обратите внимание, что размещения могут отличаться друг от друга либо только порядком следования элементов, как первые две группы, либо составом элементов, как следующие.
Формула для числа размещений.
Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Число размещений из n по m обозначается An m и определяется по формуле
An m = n·(n − 1)·(n − 2)·. ·(n − m + 1) = n!/(n − m)!
Ничего удивительного в том, что число размещений из n по n оказалось равным числу перестановок n элементов, ведь мы использовали для составления размещений всё множество элементов, а значит они уже не могут отличаться друг от друга составом элементов, только порядком их расположения, а это и есть перестановки.
Задача 3.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии 30-ти книг?
Решение.
Определим общее число размещений из 30 элементов по 15 по формуле
A30 15 = 30·29·28·. ·(30−15+1) = 30·29·28·. ·16 = 202843204931727360000.
Ответ: 202843204931727360000.
Будете размещать реальные книги? Удачи! Посчитайте, сколько жизней потребуется, чтобы перебрать все варианты.
Задача 4.
Сколькими способами можно расставить 30 книг на двух полках, если на каждой из них помещается только по 15 томов?
Решение.
Способ I.
Представим себе, что первую полку мы заполняем так же, как в предыдущей задаче. Тогда вариантов размещения из 30-ти книг по 15 будет A30 15 = 30·29·28·. ·(30−15+1) = 30·29·28·. ·16.
И при каждом размещении книг на первой полке мы еще P15 = 15! способами можем расставить книги на второй полке. Ведь для второй полки у нас осталось 15 книг на 15 мест, т.е. возможны только перестановки.
Всего способов будет A30 15 ·P15, при этом произведение всех чисел от 30 до 16 еще нужно будет умножить на произведение всех чисел от 1 до 15, получится произведение всех натуральных чисел от 1 до 30, т.е. 30!
Способ II.
Теперь представим себе, что у нас была одна длинная полка на 30 мест. Мы расставили на ней все 30 книг, а затем распилили полку на две равные части, чтобы удовлетворить условию задачи. Сколько вариантов расстановки могло быть? Столько, сколько можно сделать перестановок из 30 книг, т.е. P30 = 30!
Ответ: 30!.
Не важно, как вы решаете математическую задачу. Вы её решаете так, как представляете себе свои действия в жизненной ситуации. Важно не отступать от логики в своих рассуждениях, чтобы в любом случае получить верный ответ.
Размещения и теория вероятностей.
Задача 5.
На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинакового формата расположены в произвольном порядке. Читатель, не глядя, берет 3 книги. Какова вероятность того, что он взял первые три тома?
Решение.
Сочетания. Подсчет числа сочетаний.
Формула для числа сочетаний.
В этой формуле присутствуют два делителя и в качестве знака деления использован символ «/«, который более удобен для веб-страницы. Но деление можно также обозначать двоеточием «:» или горизонтальной чертой «−−−». В последнем случае формула выглядит как обыкновенная дробь, в которой последовательное деление представлено двумя сомножителями в знаменателе 
Кроме того, все множители и делители в этой формуле представляют собой произведения последовательных натуральных чисел, поэтому дробь хорошо сокращается, если её расписать подробно. Но подробное сокращение я в задачах пропускаю, его легко проверить самостоятельно.
Понятно, что для одинаковых исходных множеств из n элементов и одинаковых объёмов выборок (по m элементов) число сочетаний должно быть меньше, чем число размещений. Ведь при подсчёте размещений для каждой выбранной группы мы еще учитываем все перестановки выбранных m элементов, а при подсчёте сочетаний перестановки не учитываем: Сn m = An m /Pm = n!/(n−m)!/m!
Задача 6.
Сколькими способами можно расставить 15 томов на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 30-ти книг?
Решение.
Мы решаем эту задачу в контексте работы дизайнера интерьеров, поэтому порядок следования на полке 15-ти выбранных внешне одинаковых книг не имеет значения. Нужно определить общее число сочетаний из 30 элементов по 15 по формуле
С30 15 = 30!/(30 − 15)!/15! = 155117520.
Ответ: 155117520.
Задача 7.
Сколькими способами можно расставить 30 внешне неразличимых книг на двух полках, если на каждой из них помещается только по 15 томов?
Итак, бывают такие формулировки задач, что ответы могут получаться неоднозначными. Для точного решения нужна дополнительная информация, которую мы обычно получаем из контекста ситуации. Создатели экзаменационных заданий, как правило, не допускают двойного толкования условия задачи, формулируют его несколько длиннее. Однако, если у вас есть сомнения, лучше обратиться с вопросом к преподавателю.
Сочетания и теория вероятностей.
В теории вероятностей задачи на сочетания встречаются чаще всего, потому что группировка без порядка следования важнее именно для неразличимых элементов. Если какие-то элементы существенно различаются между собой, их трудно выбрать случайно, есть ориентиры для неслучайного выбора.
Задача 8.
На книжной полке находится собрание сочинений одного автора в 6 томах. Книги одинаково оформлены и расположены в произвольном порядке. Читатель берет наугад 3 книги. Какова вероятность того, что он взял первые три тома?
Решение.
Сравните эту задачу с задачей 5 (на размещения). В обоих задачах очень похожие условия и совсем одинаковые ответы. По-существу, это просто одна и та же бытовая ситуация и, соответственно, одна и та же задача, которую можно трактовать так или иначе. Главное, чтобы при подсчёте элементарных событий, как благоприятствующих, так и всех возможных, было одно и то же понимание ситуации.
Заключительные замечания.
Мы рассмотрели выборки для множества, в котором элементы не повторяются, так называемые выборки без повторений. Например, перестановки букв в слове «шляпа». Но ведь и слово «берет» нередко встречается. В этом слове от перестановки местами двух букв «е» ничего не изменится, такая перестановка не влияет на общее число всех вариантов. Понятно, что математики тоже не прошли мимо понятия выборки с повторениями и вывели соответствующие формулы для подсчёта числа вариантов. Вы можете найти их в учебниках и справочниках или посмотреть в комментариях к простым задачам здесь.
Для строгого вывода всех формул (который я здесь не приводила) используются два основных правила комбинаторики:
Понятие факториал также распространяется на ноль: 0! = 1, так как считается, что пустое множество можно упорядочить единственным способом.
Заключительная задача.
При решении задач по теории вероятностей с применением методов комбинаторики необходимо тщательно анализировать предлагаемую ситуацию, чтобы правильно выбрать тип выборки. Попробуйте сделать это на примере следующей задачи. Решите её, сравните ответ, а затем нажмите кнопку, чтобы открыть моё решение.
Задача 9.
Из аквариума, в котором 6 сазанов и 4 карпа, сачком выловили 5 рыб. Какова вероятность того, что среди них окажется 2 сазана и 3 карпа?
Решение.
Ответ: 0,238.
Если вы выпускник школы и будете сдавать ЕГЭ, то после изучения этого раздела, вернитесь к заданиям по теме «Вероятность» (10 для базового и 4 для профильного уровней ЕГЭ 2021 по математике), которые можно решать с использованием элементов комбинаторики и без неё (например, на бросание монеты). Какой из возможных способов решения задачи нравится вам больше теперь?
А если вы хотите еще немного потренироваться в решении задач комбинаторики, чтобы научиться быстро определять тип выборки и находить нужные формулы, то перейдите на страницу простые задачи.
Перейти на главную страницу сайта.
Понравились материалы сайта? Узнайте, как поддержать сайт и помочь его развитию.
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Источник
Комбинаторика
Комбинаторика – раздел математики, занимающийся изучением количества возможных комбинаций определенного типа, которые возможно сделать из некоторого набора элементов. Эти вычисления необходимы для решения различных задач в теории вероятностей и получения распределений случайных величин.
Правила в комбинаторике
Правило суммы: если есть взаимоисключающие друг друга действия A и B, которые можно выполнить способами m и n соответственно, то выполнить любое из этих действий можно m + n способами.
Правило произведения: если есть последовательность действий k, и первое действие его можно выполнить n1 способом, второе n2 и далее до nk, то все действия этой последовательности можно выполнить n1 · n2 · nk способами.
Элементы комбинаторики
Перестановки – конечное множество, в котором указан порядок его элементов. Количество перестановок вычисляется по формуле: Pn = n!
Калькулятор разложения бинома Ньютона с использованием треугольника Паскаля.
Калькулятор числа перестановок позволяет вычислить число возможных сочетаний из заданного количества элементов.
Калькулятор числа размещений вычисляет число возможных размещений из заданного количества объектов n по k.
Калькулятор числа сочетаний позволяет вычислить число возможных сочетаний из заданного количества объектов n по k.
Источник